Objects in a Uniform Magnetic Field via IABCs
David Meeker
dmeeker@ieee.org
22Nov3018
1 Introduction
Several problems of interest in magnetics involve the modeling of an object in a uniform, unbounded magnetic field. Since a finite element model generally only solves magnetic problems on a bounded domain, it would appear to be difficult to approximate this condition using FEMM. However, it is possible to combine immersion in a constant magnetic field with an unbounded domain using Improvised Asymptotic Boundary Conditions (IABCs) in FEMM. This note shows how to modify the IABCs that are automatically generated by FEMM in order to establish a constant magnetic field.
Improvised Asymptotic Boundary Conditions
IABCs are a method of approximating unbounded domains with FEMM. The method uses several layers of varying permeability at the outer edges of a circular solution domain to accurately emulate the impedance of an unbounded domain. An example implementation is shown in Figure 1. The automatic creation of IABCs in FEMM is described on the OpenBoundaryExample page.
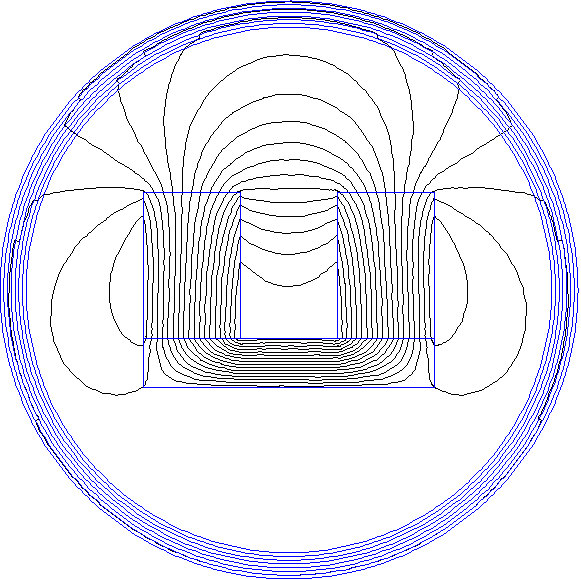
Figure 1: Open boundary solution via IABCs.
Uniform Field in an Axisymmetric Domain
A classical result in electromagnetics is the solution for the field of a uniformly magnetized sphere in an unbounded space (see, for example, [1], p329). This situation is shown below as Figure 1.
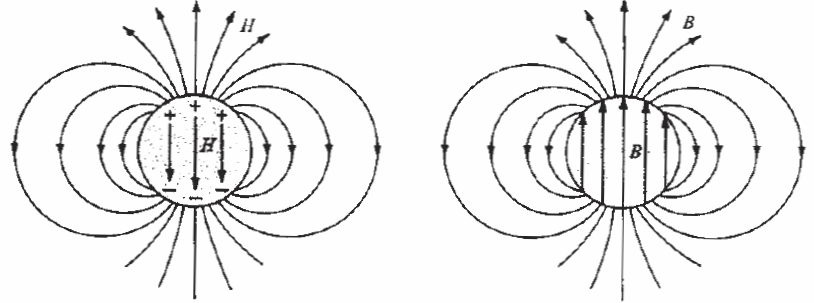
Figure 2: B and H in a uniformly magnetized sphere (from [1]).
In this situation, the B and H fields are parallel and uniform inside the sphere, which is a property of the spherical shape. If the sphere has an internal relative permeability of \(\mu_o\) and a coercivity of \(H_c\), [1] shows that the sphere has a uniform flux density of:
\[ \label{eq1} B_{sphere} = \frac{2}{3}\mu_o H_c\]
To obtain a given flux density inside the sphere, the associated \(H_c\) would be:
\[\label{eq2} H_c = \frac{3}{2} \frac{B_{sphere}}{\mu_o}\]
Now, a spherical region with an IABC could be considered to be like a uniformly magnetized sphere in an unbounded region (i.e. created by the IABC). However, in the default IABC implementation, there is no magnetization defined for the sphere. This magnetization can be defined by specifying \(H_c\) for each of the materials associated with external region. The \(H_c\) specified for each external region material (u1 ... un) should be specified per \(\ref{eq2}\) and magnetization direction of each block label associated with each layer of the exterior region should be set to either 90o or -90o. The definition of these \(H_c\) values creates the same current distribution on the surface of the interior region as would be present if the sphere were uniformly magnetized.
The example uniform_field_axi.FEM demonstrates an implementation of this strategy. A value of \(H_c = \frac{1}{\mu_o}\) was specified for each external material. The resulting solution is shown below as Figure 3. The Figure shows straight field lines, and querying any point in the interior region yields a field of 0.666609 Tesla, very close to the theoretical value of 2/3 Tesla.
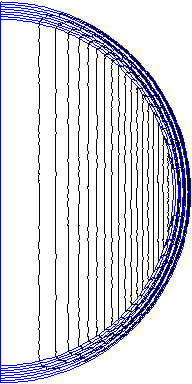
Figure 3: Uniform axisymmetric field created with IABCs.
Uniform Field in a 2D Planar Domain
The same idea applies for a uniformly magnetized circle in a 2D domain as for a uniformly magnetized sphere in an axisymmetric domain. However, whereas the demagnetization factor for a sphere is 1/3, the demagnetization factor of a circle in a 2D domain is 1/2. This demagnetization factor leads to the prescription for the external region \H_c\) of \(\ref{eq3}\):
\[\label{eq3} H_c = \frac{2}{\mu_o} B_{circle}\]
The file uniform_field_2d.FEM is a demonstration of the 2d-planar implementation. Again, A value of \(H_c = \frac{1}{\mu_o}\) was specified for each external material. The resulting solution is shown below as Figure 4. The field inside the interior region is a uniform value of 0.499966 Tesla, very close to the theoretical solution of 1/2 Tesla.

Figure 4: Uniform 2D field created with IABCs.
Conclusions
In both the 2D and axisymmetric cases, the reaction field created by any objects in the interior region will act the the same way as objects in an unbounded space due to the effects of the IABC structure. The approach described in this note is a simple way to emulate exposure of objects to a uniform external magnetic field in an unbounded region with FEMM.
References
[1] M. Plonus, Applied Electromagnetics, McGraw-Hill, 1978.
| File | Last modified | Size |
|---|---|---|
| uniform_field_2d.FEM | 2018-11-22 13:11 | 5Kb |
| uniform_field_axi.FEM | 2018-11-22 13:11 | 5Kb |