Steady-State Analysis of Compumag TEAM Problem 28
David Meeker
April 27, 2006
1 Introduction
This note describes the analysis of the Compumag TEAM Problem 28. This problem concerns the modeling of an electrodynamic device consisting of two stationary concentric air-cored coils interacting with a moveable round aluminum plate. The problem's detailed geometry is shown below in Figures 1 and 2 (borrowed from the TEAM problem definition):

Figure 1: Problem 28 geometry.
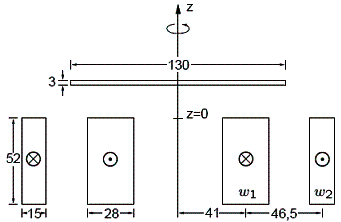
Figure 2: Machine dimensions in millimeters.
Whereas the Problem 28 seeks to model the transient behavior of the device, the present FEMM model will only seek to investigate the steady-state levitation height reported in the problem description.
2 FEMM Problem Definition
Two models of this problem are available. The first model, team28a, uses an “asymptotic boundary condition” to terminate the solution region. The second model, team28k, uses the “Kelvin transformation” which paradoxically explicitly models unbounded free space while solving over a finite computational region. Both of these "open boundary" techniques are described in a survey paper by Chen and Konrad.
Both in both of these models, a Circuit Property, denoted “icoil”, is defined. Since the circuit is applied to multi-turn coil regions, the circuit type is set to “parallel”. A current of 20 A is specified, consistent with the Team 28 problem definition. Although the specific wire gauge, etc., is not specified in the problem definition, it is assumed that the coil is wound out of 18 AWG copper magnet wire. The resulting fill factors for the coils are then feasible (54.3% and 60.8% for the inner and outer coils, respectively). Defining the windings in this fashion allows FEMM to compute various properties of the winding (e.g. terminal voltage, impedance, flux linkage) automatically. With this sort of bulk coil definition, FEMM also automatically includes a continuum model of proximity and skin effects in the coils (although in this particular problem, proximity and skin effect losses are relatively trivial).
Since TEAM 28 is an “open circuit” problem, there is no “natural” outer boundary of the solution region. Ideally, one would like to solve for the magnetic fields in all of free space; however, the finite element method is based upon discretizing and solving the magnetic field over a finite domain. Therefore, the method by which the solution region is cropped to a finite domain has important implications on the accuracy of the resulting solution.
The team28a model uses an “asymptotic boundary condition.” This model is pictured below in Figure 1. To implement this method, a spherical solution region is first required. An impedance boundary condition:
![]()
(where n represents the outward normal to the spherical region and R represents the radius of the region) is applied to the edge of the solution region. This boundary condition is described in more detail in Appendix A.3.2 of the FEMM Manual. This boundary condition approximately represents the impedance of the external region (i.e. only takes account of first spatial harmonic of the magnetic field), but as long as the boundary isn’t too close to the objects of interest, the approximation is generally both computationally economical and highly accurate.
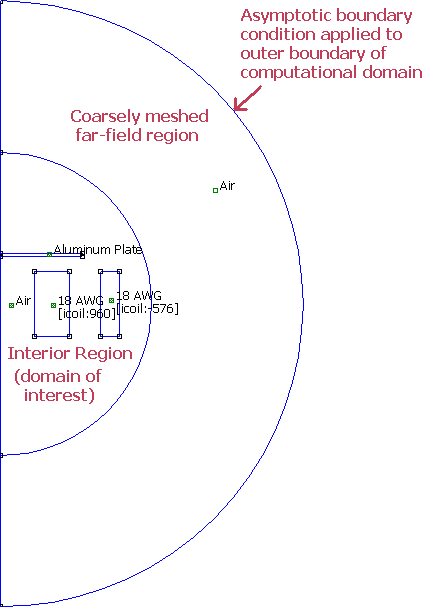
Figure 1: The team28a model that approximates an unbounded solution region with an impedance boundary condition applied to the outer edge of the solution region.
The team28k model uses a conformal mapping strategy called the “Kelvin Transformation”. This model is pictured below in Figure 2. Again, a spherical solution region is required for the “domain of interest”. However, a second spherical region is also modeled. The Kelvin Transformation maps the entirety of the unbounded external region onto the second spherical region. The outer edge of the “domain of interest” is linked with the outer edge of the second sphere with a periodic boundary condition. For axisymmetric problems, the permeability of the external region must vary with the distance from the center of the external region for an accurate mapping. FEMM can automatically vary the permeability in the external region if:
ü The region is specified as an external region by selecting the “Block located in an external region” check box in the properties dialog for the block label that is associated with the external region.
ü The dimensions of the internal and exterior regions are summarized in the “Exterior Region Properties” dialog. This dialog is appears if “Properties|Exterior Region” is selected off of the magnetics preprocessor main menu.
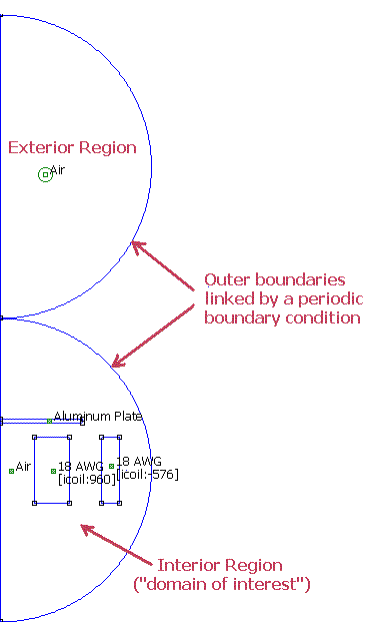
Figure 2: The team28k model that uses the Kelvin Transformation to model an unbounded solution domain.
Generally, the external region can be relatively coarsely meshed, so there is a relatively low computational cost for this method. This method is the most accurate way to treat an unbounded problem, because the entire external region is explicitly modeled. Since the entire external region is explicitly modeled, the boundaries of the internal region can be drawn arbitrarily close to the objects of interest without introducing error.
3 Analysis Results - Force
In the Team 28 problem definition, the measured steady-state levitation position of the aluminum plate is 11.3 mm. Both FEMM models locate the aluminum plate at this position. The mass of the plate is quoted to be 0.107 kg, implying a that the force on the plate should be very close to 1.05 N at this position.
This particular problem is amenable to several different force computation methods. Since the aluminum plate has the same permeability as air, force on the plate can be computed by integrating the Lorentz force on the induced currents in the plate. In instances where the Lorentz force computation is applicable, this method tends to provide the most accurate results.
Alternatively, force can be computed by selecting the aluminum plate and evaluating the "weighted stress tensor" volume integral. This method computes force via Maxwell's stress tensor, but it evaluates the stress tensor integral as a volume integral that essentially averages the results of multiple stress tensor integration paths, resulting in a more accurate computation than the Maxwell stress tensor line integral. Results for various force computation methods at various mesh densities are presented in Table 1.
|
team28k |
team28a |
||||
|
# nodes |
Lorentz |
WST |
# nodes |
Lorentz |
WST |
|
16282 |
0.998867 N |
0.967554 N |
16575 |
1.00067 N |
0.970327 N |
|
62201 |
1.00503 N |
0.999116 N |
63679 |
1.00559 N |
1.00031 N |
|
243345 |
1.00643 N |
1.00495 N |
249360 |
1.00670 N |
1.00517 N |
|
960063 |
1.00676 N |
1.00623 N |
987616 |
1.00693 N |
1.00641 N |
Table 1: Force calculated with different methods at different mesh densities.
In this case, both models predict just about the same force. The Lorentz force calculation appears to converge a bit faster with increasing mesh size than the weighted stress tensor.
Analysis Results – Impedance & Losses
Interesting circuit-related properties are obtained by pressing the inductor button on the postprocessor toolbar. The dialog pictured in Figure 3 then appears.
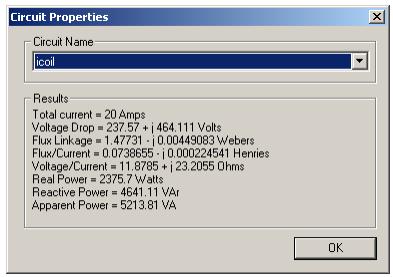
Figure 3: Circuit results from the team28k model.
By performing volume integrals over various regions in the problem, one can understand the various mechanisms that compose these bulk circuit results. For example, one could seek to identify the various loss components of the reported real power. The three relevant mechanisms in this model are summarized in Table 2.
|
Resistive losses in coils |
2361.59 W |
|
Proximity effect losses in coils |
0.914029 W |
|
Resistive losses in aluminum plate |
13.1981 W |
|
Total losses |
2375.7 W |
Table 2: Loss break-down in the team28k model.
4 Conclusions
The Compumag TEAM 28 problem has been analyzed in its reported steady-state levitation position. Two different methods of dealing with the unbounded nature of this problem were presented, and similar results were obtained with each method. Computed forces were a reasonable match to the force expected (i.e. to offset the plate's weight) at this position. The impedance and losses associated with the system were also computed.
References
Q. Chen and A. Konrad, “A review of finite element open boundary techniques for static and quasistatic electromagnetic field problems,” IEEE Transactions on Magnetics, 33(1):663-676, January 1997.