Radial Magnetic Bearing Example (Nonlinear Magnetostatics)
David Meeker
September 11, 1999
This example refers to the example file brgmodel.fem
Introduction
Magnetic bearings are used to in lieu of rolling element or fluid film journal bearings in some high performance turbomachinery applications. Specific applications include pumps for hazardous/caustic fluids, precision machining spindles, energy storage flywheels, and high reliability pumps and compressors.
Magnetic bearings yield several advantages. Since there is no mechanical contact in magnetic bearings, mechanical friction losses are eliminated. In addition, reliability can be increased because there is no mechanical wear.
Besides the obvious benefits of eliminating friction, magnetic bearings also allow some perhaps less obvious improvements in performance. Magnetic bearings are generally open-loop unstable, which means that active electronic feedback is required for the bearings to operate stably. However, the requirement of feedback control actually brings great flexibility into the dynamic response of the bearings. By changing controller gains or strategies, the bearings can be made to have virtually any desired closed-loop characteristics. Forexample, flywheel bearings are extremely compliant, so that the flywheel can spin about its inertial axis--the bearings serve only to correct large, low-frequency displacements. Conversely, magnetic bearings in machining spindles must be extremely stiff and have a very broad bandwidth so that tool position is accurately controlled. In each case, the dynamic response is a result of the controller used to stabilize the bearing, rather than a consequence of the bearing's physical design.
Typical Bearing Geometry
Conceptually, the typical magnetic bearing is composed of four of horseshoe-shaped electromagnets. This configuration is shown in Figure 1. The four magnets are arranged evenly around a circular piece of iron mounted on the shaft that is to be levitated. Each of the electromagnets can only produce a force that attracts the rotor iron to it, so all four electromagnets must act in concert to produce a force of arbitrary magnitude and direction on the rotor.
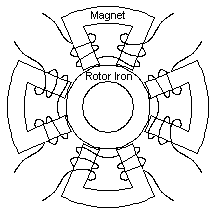
Figure 1: Magnetic bearing composed of four discrete horseshoes
For structural strength and manufacturability, this sort of magnetic bearing is manufactured with iron connecting the horseshoes, so that the stator iron is one monolithic piece. This geometry is shown in Figure 2.
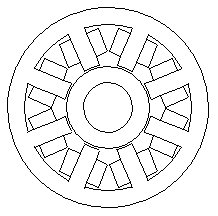
Figure 2: Eight-pole magnetic bearing.
There are N turns of wire around each leg of the bearing. So that the bearing behaves functionally like a bearing composed of discrete horseshoes, sets of adjacent coils are connected together in reverse series, just as pictured in Figure 1.
Flux Density and Force from Circuit Theory
This type of magnetic bearing is amenable to analysis via magnetic circuit theory. Assuming negligible leakage and fringing and neglecting the small reluctance of the iron parts of the flux path yields the following magnetic circuit:
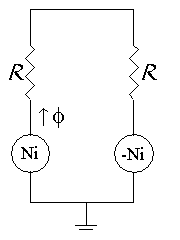
Figure 3: Magnetic circuit for a horseshoe.
Figure 3 looks just like an electric circuit with batteries and resistors. However, instead of current, there is flux φ, and instead of resistance, there is reluctance R. Rather than voltage sources, there are magnetomotive force (MMF) sources of strength Ni and -Ni. In terms of the geometry of the bearing, the reluctance is:
![]()
where g is the nominal air gap between the rotor and the tip of each leg of the bearing, a is the cross-sectional area of each leg, and μo is the permeability of free space (1.2566e-6 Tesla*Meter/Amp). One can solve for the flux in the circuit:
![]()
The flux density, B, in the airgap is the flux divided by the area of the airgap:
![]()
We can now use Maxwell's Stress Tensor to figure out the force. For each horseshoe, the force in terms of flux in the gap is, from the Stress Tensor:
![]()
Substituting in the expression determined for B yields:
![]()
In addition, the flux density obtainable in the gap should be limited by the flux that can get down the legs of the bearing. Say that the core material saturates at a force of Bsat. Then, the maximum force that can be produced by the a particular bearing geometry is:
![]()
For the purposes of bearing design, useful corollary results are the maximum current required in a horseshoe:
![]()
and the inductance of a horseshoe:
![]()
Control Via Bias Current Linearization
Now, consider two opposed horseshoes, as pictured in Figure 4, working together to produce forces along one axis of the bearing. Rearranging the above expressions for force and current a bit yields, when both currents are taken into account and the rotor is centered in the bearing:
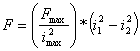
For control purposes, this form is not so good. It is highly desirable to have a linear relationship between the input and the resulting force, so that the usual controller design tools can be applied.
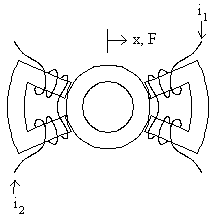
Figure 4: One axis of a horseshoe-configured bearing
Fortunately, the relationship can be converted into a bilinear form with a change of variables. The currents i1 and i2 can be thought of as being composed of a constant "biasing" component that doesn't produce any force, in combination with a "perturbation" component that is proportional to the desired force:
![]()
![]()
To get the maximum load capacity out of the bearing, one sets
![]()
With this choice of bias, when the maximum force is being produced by one horseshoe, the opposing horseshoe produces no force at all. Substituting the new definitions for current into the expression for force yields:
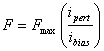
With a little more algebraic manipulation, it is possible to linearize the force about the centered position to get the dependence of the force on position as well, when the above bias current linearization scheme is employed. The result is:
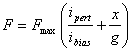
where x represents the distance that the rotor is displaced from the centered position. The same analysis can be applied to the two horseshoes that produce vertical forces as well.
Design Verification with Finite Element Analysis
The above equations provide a basis for the rough preliminary design of magnetic bearings. However, there are several effects that we have neglected in favor of obtaining simple, approximate design equations:
- Neglected the (nonlinear) reluctance of the iron sections of the flux path;
- Neglected leakage flux that tends to saturate the legs of the bearing earlier than one would be lead to believe on the basis of circuit theory, as well as increase the inductance of the bearing;
- Neglected fringing effects (flux going out of the sides of the legs), which again changes the actual force produced by the bearing, and also tends to lead to premature saturation in the bearing's legs;
- Neglected eddy current effects, which change the dynamic response of the bearing. The eddy currents ultimately impose limits on the frequencies at which the bearing can produce useable force.
The usual approach is to design a bearing from formulas like the above design equations, and then "fine-tune" the design with a more elaborate finite element analysis that brings the secondary effects into evidence.
Example Geometry
As an example, consider the nominal geometry listed in Table 1:
|
Air Gap Length |
1 mm (0.04") |
|
Pole Width |
1 cm (0.4") |
|
Axial Length of Core |
4 cm (1.6") |
|
Turns per Leg |
80 turns of 18 AWG |
|
Max. Airgap Flux Density |
1.2 Tesla |
Table 1: A nominal magnetic bearing design.
The above design formulas can be applied to these parameters to predict the bearing's performance. The estimated performance results are compiled in Table 2.
|
Maximum Force |
460 N |
|
Maximum Current |
12 A |
|
Bias Current |
6 A |
|
Open-Loop Stiffness |
-460,000 N/m |
|
Inductance per quadrant |
6.4 mH |
Table 2: Estimated performance from design equations.
To make a valid geometry for analysis, a few more details about the bearing must be specified. It is also assumed that:
- The core is composed of M-19 steel laminations 14 mils thick with a packing factor of 0.98;
- The bearing is mounted on a 1.2" diameter shaft;
- The bearing is to be operated with a NNSS biasing scheme, requiring the legs and backiron of the bearing to be approximately the same thickness;
- The 80 turns are evenly distributed in a "bulk" conductor of approximately 0.3" x 0.6"
The detailed geometry used by the finite element analysis is pictured in Figure 5. Some small variation on the nominal geometry (on the order of 1% on some dimensions) have been made to make the geometry fit together easier.
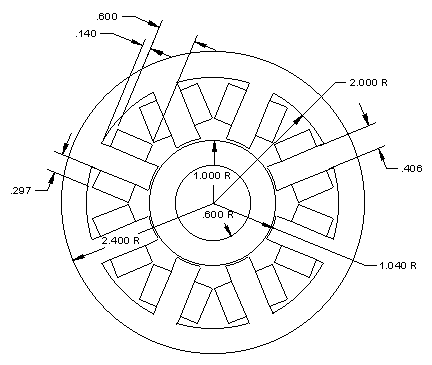
Figure 5: Actual bearing geometry to be analyzed (dimensions in inches)
The case of interest in the example simulation is the production of the maximum design vertical force. Currents in the left and right quadrants are chosen to be half the maximum current (the bias current level). Current in the top quadrant is chosen to be the imax, and current in the bottom quadrant is chosen to be zero.
The results of the simulation are pictured in Figure 6.
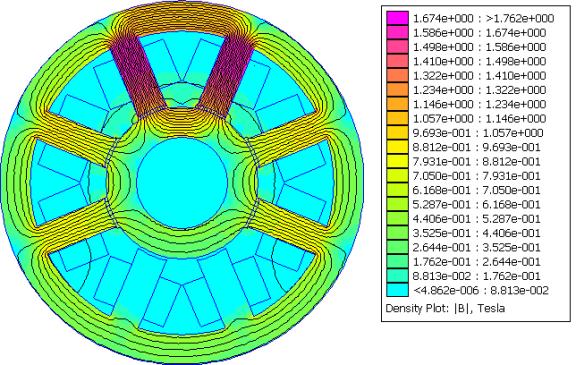
Figure 6: Simulation results for maximum upward force.
Forces are obtained by selecting the rotor in block integral mode and evaluating the force on the rotor via "weighted stress tensor" method volume integral. This method typically produces more accurate results than integrating the Maxwell's Stress Tensor line integral on a closed path encircling the rotor. The "weighted stress tensor" integral reports a force of 400N.
This result is only 87% of the force predicted by the design equations. However, a careful examination of the results shows the cause of the difference. Looking at Figure 6, one can see that flux levels are higher in the middle of the legs than at the pole tips. By switching into "Point" mode and looking at the flux values at the middle of the either of the upper legs yields values in the neighborhood of 1.59 Tesla, and the relative permeability of the iron is only about 350. In the center of either of the upper air gaps, the flux is 1.1 Tesla rather than 1.2 T. The implication here is fringing flux is causing undesirable premature saturation. The legs are saturating, making less total flux go down the legs per unit of coil current than occurs at lower current levels. However, even though the flux is a high 1.59 T in the center of the legs, the flux level is only 1.1 T in the gap, because a substantial portion of the flux (the fringing flux) exits the sides of the legs, rather than at the pole tips.
Conclusions
This example demonstrates one of the more valuable uses of finite element analysis--validating and refining a design obtained by simpler analytical formulas. This particular example represents the application of the Finite Element Method Magnetics program to a nonlinear problem in magnetostatics.