Example Element-by-Element Block Integral Calculation
A number of block integrals come predefined in FEMM for easy calculation in the postprocessor. Unfortunately, the finite variety of integrals does not cover every possible situation that the power user may desire. In the case that the desired integral is not directly built in to FEMM, it is possible to use a simple script to compute the desired integral on an element-by-element basis, summing the results from each element to get the desired integral result.
The element-by-element integral functionality is possible due to the mo_numnodes, mo_numelements, mo_getnode, and mo_getelement commands (and related commands for problem types other than magnetic ones) that were added in the 15Jul2009 release of FEMM. These functions allow the user to have direct access to the node and element information. This information can then be used as part of a numerical integration over the region of interest.
As a specific example of the use of this approach, consider the solution pictured below in Figure 1. Assume that, for some reason, one wants to compute the magnetic field energy stored in the rotor of the machine (the region lit up in green in Figure 1) explicitly via an element-by-element block integral, rather than by simply using the built-in "Magnetic field energy" block integral.
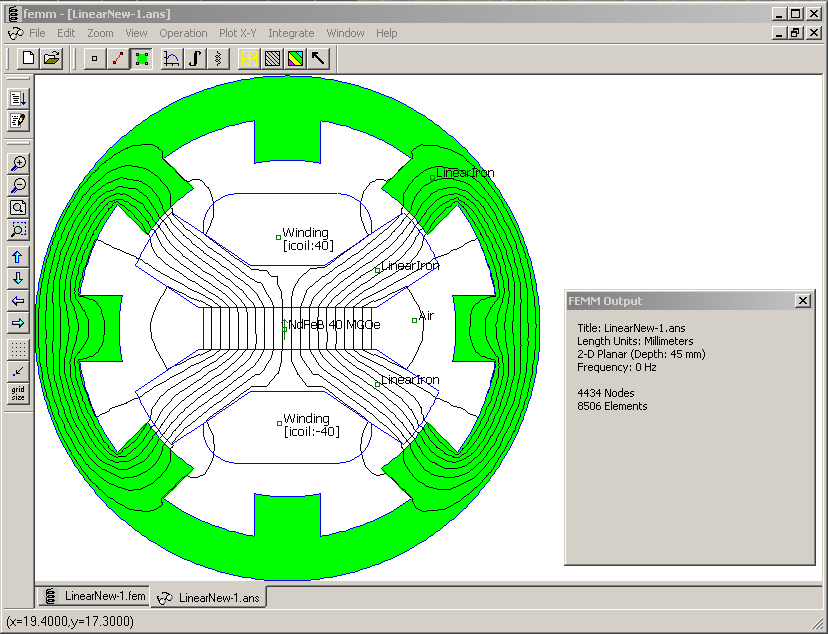
Figure 1: Element-by-Element Block Integral example geometry.
For a magnetically linear region, the definition of the magnetic stored energy, wm, is (see http://farside.ph.utexas.edu/teaching/em/lectures/node78.html#e6en, for example, as a reference):
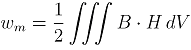
Below is a script that “manually” computes stored energy on an element-by-element basis and then compares the result to that obtained using the built-in integral. The script cycles through all of the elements in the geometry. The rotor elements have been labeled, when the example geometry was created, as being in Group 1. The example code uses the group number to tell which elements to include in the integral. When cycling through the elements, the mo_getelement function tells the script the location of the centroid of each element and the size of each element. With the formulation that FEMM uses, quantities like flux density and field intensity are piece-wise constant over an element, so it is sufficient to simply evaluate the mo_getpointvalues function at the centroid of an element and assume that the values are piece-wise constant over the element for the purposes of computing the integral.
open("LinearNew.fem");
mi_analyze();
mi_loadsolution();
-- Turn off smoothing so that mo_getpointvalues will return the
-- "raw" piece-wise constant values for flux density and field intensity
mo_smooth("off");
-- Grab the total number of elements in the problem;
numelm = mo_numelements();
-- Call mo_getprobleminfo to grab the depth of the problem in th
-- into-the-page direction, which we need for computing volume integrals.
-- Note that the problem depth is always returned in units of meters.
problemtype,freq,depth=mo_getprobleminfo()
-- Loop through all elements to evaluate the stored energy in all regions
-- denoted as being part of Group 1.
nrg = 0;
for k=1,numelm do
p1,p2,p3,x,y,a,g=mo_getelement(k);
if (g == 1) then
-- Compute element volume.
dv = depth*a*mm^2;
-- Evaluate properties at element centroid
a,bx,by,Sig,E,hx,hy = mo_getpointvalues(x,y);
-- Compute the contribution of this element to the integral
nrg = nrg + (1/2)*(bx*hx+by*hy)*dv;
end
end
-- For comparison, directly select Group 1 and perform the integral using
-- the built-in function
mo_groupselectblock(1);
altnrg = mo_blockintegral(2);
-- Print out results
print("Energy in group 1 computed by manual integral ",nrg);
print("Energy in group 1 computed by canned integral ",altnrg);
mi_analyze();
mi_loadsolution();
-- Turn off smoothing so that mo_getpointvalues will return the
-- "raw" piece-wise constant values for flux density and field intensity
mo_smooth("off");
-- Grab the total number of elements in the problem;
numelm = mo_numelements();
-- Call mo_getprobleminfo to grab the depth of the problem in th
-- into-the-page direction, which we need for computing volume integrals.
-- Note that the problem depth is always returned in units of meters.
problemtype,freq,depth=mo_getprobleminfo()
-- Loop through all elements to evaluate the stored energy in all regions
-- denoted as being part of Group 1.
nrg = 0;
for k=1,numelm do
p1,p2,p3,x,y,a,g=mo_getelement(k);
if (g == 1) then
-- Compute element volume.
dv = depth*a*mm^2;
-- Evaluate properties at element centroid
a,bx,by,Sig,E,hx,hy = mo_getpointvalues(x,y);
-- Compute the contribution of this element to the integral
nrg = nrg + (1/2)*(bx*hx+by*hy)*dv;
end
end
-- For comparison, directly select Group 1 and perform the integral using
-- the built-in function
mo_groupselectblock(1);
altnrg = mo_blockintegral(2);
-- Print out results
print("Energy in group 1 computed by manual integral ",nrg);
print("Energy in group 1 computed by canned integral ",altnrg);
When the script is run, the script prints the results from both the manual element-by-element integral and the automatically computed integral. The results are of the manual and automatic integral calculations are identical.
An archive containing both the lua script and example geometry is available at https://www.femm.info/examples/integral/IntegralExample.zip.