Meshing Heuristics for Improved Convergence
David Meeker
16Oct2011
1) Introduction
In a recent conference presentation, the convergence of FEMM was compared to several other programs, including several solvers with various sorts of adaptive mesh refinement. Some recent changes have been made to improve the convergence of FEMM by changes to the meshing. While the program does not use adaptive meshing, several heuristics have been added to the mesh generation. These changes result in convergence that is similar to programs with adaptive meshing on 1st order triangular elements. This note will explain the recently added heuristics; describe a benchmark problem used for convergence comparison, and demonstrate the convergence results of the revised code.
2) Benchmark Problem
The problem under consideration is a linear electrostatic problem. The problem consists of an axisymmetric domain with a conductive cone and sphere. The cone is held at 1kV and the sphere is held at ground. The goal is to determine the stored energy in the problem domain. The detailed dimensions and positioning of the objects the domain are pictured in Figure 1.
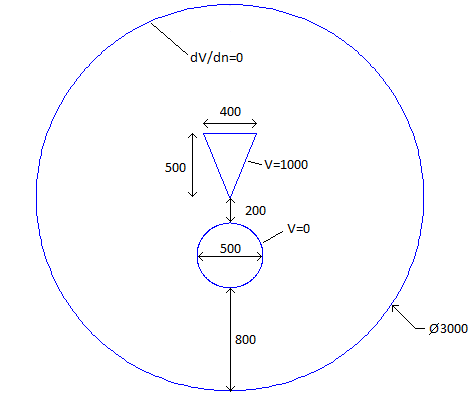
Figure 1: Benchmark problem domain.
The convergence of various solvers on this domain, reproduced from Dolezel et al., is shown in Figure 2.
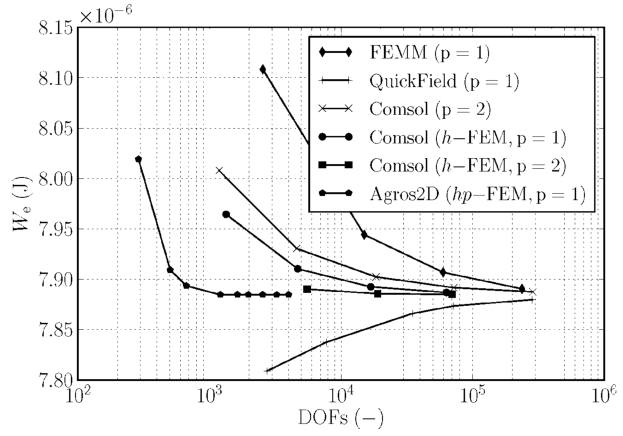
Figure 2: Convergence of energy calculation on benchmark problem for various solvers.
As shown in Figure 2, the convergence of FEMM is slow relative to adaptive solvers. Although the program gives reasonable answers, it takes a large number of elements to converge to the correct solution with high accuracy.
3) New Meshing Heuristics
The reason why adaptive solvers do well in this sort of problem is that there are regions of very high E near the sharp edge at the base of the cone and near its point. As shown in Figure 3, adaptive solvers achieve faster convergence by highly refining the mesh near these corners.
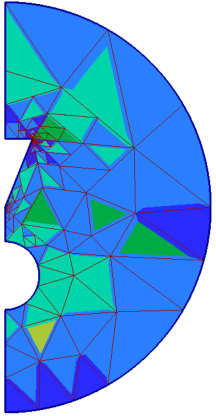
Figure 3: 1st order adaptive triangle mesh generated by Agros2D.
Although it is clear that fine meshing will be needed near corners in the domain, Triangle, the mesh generator used by FEMM, gives the corners no special treatment. By default it tries to make a mesh with the least possible number of nodes, enforcing constraints on the minimum angles in the triangles in the mesh.
In light of these insights, recently implemented heuristics meant to improve convergence are:
- Force Fine Meshing in All Corners. The 01Oct2011 version of the program forces finer meshing by placing additional points near corners before the geometry is sent to Triangle for meshing. In combination with a large minimum angle constraint, this forces Triangle to produce finely meshed corners.
- Define and Enforce a Maximum Mesh Size. In previous builds, if the default mesh size was selected for a region, the results were generally too coarse to provide accurate answers. Now, the 01Oct2011 version computes a bounding box for the domain. A maximum allowable mesh size is then computed as 1% of the length of the diagonal of the bounding box. For example, if the domain is an empty square, this heuristic generates a default mesh with about 4200 elements.
- Suggest a Finer Default Discretization for Arc Segments. Previously, a 5 degree default was suggested when arcs were drawn. The 01Oct2011 suggests 1 degree instead. With a finer discretization, errors associated with approximating arcs with a series of straight lines are minimized.
A FEMM problem definition, sparkgap.fee has been generated that corresponds to the geometry in Figure 1. The default mesh from the 09Nov2010 build is shown as Figure 4. The mesh contains about 275 nodes. The mesh near the corners is particularly coarse--the mesh generator produces little refinement, since the input geometry meets the mesher's minimum angle constraints.
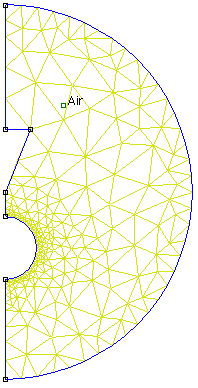
Figure 4: Default mesh for benchmark problem from 09Nov2010.
A default mesh from the 01Oct2011 build looks as pictured in Figure 5. This mesh has 3575 nodes. As shown on the inset in Figure 5, the sharp corners are now finely meshed, moving to the default mesh spacing with a fairly gradual mesh grading.
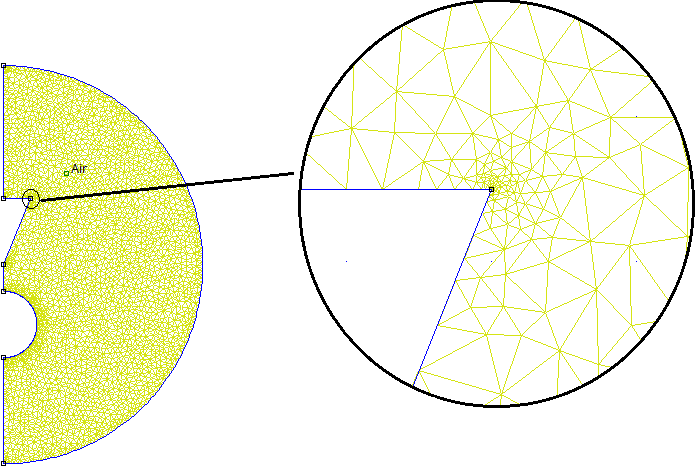
Figure 5: Default mesh for benchmark problem from 01Oct2011.
4) Results
The benchmark problem was simulated multiple times with FEMM 4.2 01Oct2011. The results are shown in Table 1. The first entry is the default mesh (i.e. when no mesh density is explicitly specified). Each subsequent mesh was generated by pressing <F3> in the FEMM user interface to reduce the mesh size by 1/2, which approximately results in a 4X increase in the number of nodes.
| Nodes | Energy, μJ |
| 3575 | 7.92563 |
| 10696 | 7.89990 |
| 39404 | 7.88835 |
| 153883 | 7.88348 |
| 614205 | 7.88152 |
Table 1: Energy results for various mesh densities.
The convergence of the revised method is superimposed on the previously presented convergence plot as the red line in Figure 6. With the meshing heuristics employed, the convergence of FEMM vs. the number of elements is similar to a p=1 h-adaptive scheme, and even the coarsest allowable mesh generates a result that is within 1% of the high mesh density result.
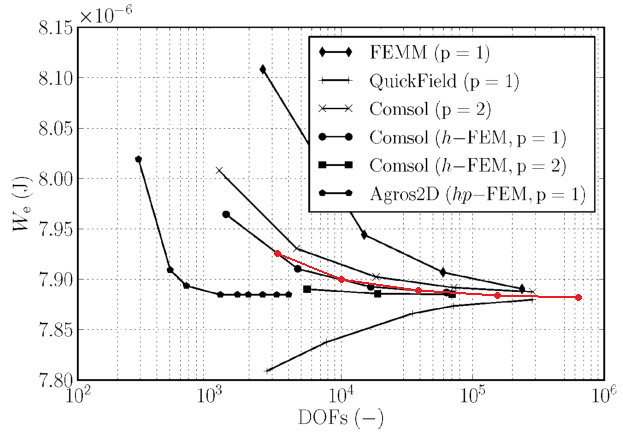
Figure 6: Plot showing performance of revised meshing strategy.
5) Conclusions
FEMM 4.2 01Oct2011 includes new meshing heuristics that improve the convergence of important post-processed quantities like force, torque, and energy. In the benchmark example considered in this note, convergence similar to that of an adaptive solver is automatically obtained by the program. Although not presented here, good results have also been obtained for force and torque in magnetic problems where the new meshing heuristics were employed.