Calculation of Rotational Losses in Heteropolar Magnetic Bearings with FEMM

David Meeker

07 Mar 2006

(Updated 06 Aug 2014 with windage)

Introduction

An important advantage of magnetic bearings is their potential for reduced rotational losses relative to rolling element and fluid film bearings. To realize this potential, it is important to have a reasonably accurate method of predicting the rotating losses, both to quantify the improvement in design studies and to account for losses in the final design.

In [1], a rotating loss model is described that accounts for rotating losses due to both hysteresis and eddy current effects. This previous work solves analytically for eddy currents in the moving rotor, ultimately presenting a set of impedance boundary conditions that must be satisfied on the surface of the rotor. A model of the rest of the bearing is then solved, subject to these boundary conditions on the surface of the rotor. The rotating losses can then be inferred from magnetic field solution in the air around the rotor.

Although this previous work produces results that compare well to experimental data, it has two shortcomings of that limit its practical applicability:

The impedance boundary conditions in [1] are written in terms of magnetic scalar potential. In contrast, most magnetic finite element solvers employ a magnetic vector potential-based formulation.
The impedance boundary conditions related the amplitude and phase of each spatial harmonic of potential at the rotor’s surface to the amplitude and phase of the normal derivative of potential that the rotor’s surface. Although most magnetic finite element solvers allow impedance-type boundary conditions, these boundary conditions are applied on a element-by-element basis, not on a harmonic-by-harmonic basis.

This note describes the creation of an Octave worksheet that solves for rotating losses using FEMM as a finite element engine. To accommodate FEMM’s vector potential-based formulation, vector potential versions of the harmonic boundary conditions and the related loss expression are presented. Octave then is used to convert the harmonic boundary conditions into a set of Neumann boundary conditions that are applied iteratively on an element-by-element basis over the surface of the rotor.

Vector Potential Boundary Condition

The boundary condition developed in [1] applies to the air adjacent to the rotor’s surface. Although [1] models the magnetic field in air using magnetic scalar potential, the magnetic field in air could be equally well described in terms of magnetic vector potential, i.e.

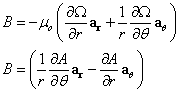
where \(\Omega\) represents magnetic scalar potential and A represents magnetic vector potential. For each spatial harmonic of the field, the sinusoidal field variation with angular position can be used to write the derivative in the q direction in terms of potential as:

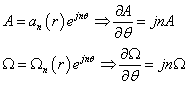
By comparing the two expressions for flux density, scalar potential can be written in terms of vector potential for each harmonic. These expressions can then be substituted into the impedance boundary condition (15) in [1] to obtain the impedance boundary condition in terms of vector potential:

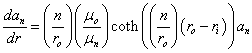
where a_nis a complex number representing the amplitude and phase n^th spatial harmonic of vector potential, m_n represents the magnet permeability of the n^th spatial harmonic (as defined in [1]), and r_i and r_o are the inner and outer radii of the rotor, respectively.

In a similar way, the rotating loss per unit of axial bearing length can be obtained by converting (21) from [1] as:

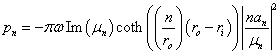
Iterative Implementation in FEMM

The conversion between spatial and harmonic coordinates is described in [2]. To apply the harmonic boundary condition, this transformation is applied to values of potential, A, measured on the rotor’s surface to obtain the amplitude and phase of each harmonic of A (i.e. a sequence of a_n's). These values are then used to produce the normal derivative of potential to be applied for the next solution iteration, i.e.:

These results are converted back into normal derivatives on the surface of the rotor for application to individual elements on the rotor's surface in FEMM.

Windage Losses

Aside from hysteresis and eddy current losses, windage losses are another significant component of rotating losses in magnetic bearings. An expression for windage loss on a rotating cylinder inside a concentric stationary cylinder is given in NASA TN D-4849, "Prediction of windage power loss in alternators."

\[Windage \, Loss = \pi C_d \rho r_o^4 \omega^3 L \]

where \(\rho\) is the density of air; \(\omega \) is the speed of the rotor; \(L\) is the axial length of the rotor; and \(C_d\) is the drag coefficient of the rotor. The drag coefficient is obtained by solving the equation:

\[\frac{1}{\sqrt{C_d}} = 2.04 + 1.768 \ln \left( Re \sqrt{C_d} \right) \]

and Reynolds Number \(Re\) is defined as:

\[ Re = \frac{r_o\,g\,\omega}{\nu}\]

where \(\nu\) is the kinematic viscosity of air and \(g\) is the clearance between the rotor surface and the pole tips.

FEMM Implementation

An example FEMM implementation is the Octave script brgloss.m. Octave is a matrix analysis program that is "mostly compatible with Matlab". This script is used in conjunction with the OctaveFEMM package included in the FEMM distribution. This package allows Matlab or Octave to manipulate FEMM in a similar fashion as the built-in Lua scripting language. However, Matlab/Octave’s support of matrices and complex numbers makes it easier to implement the transforms between point values and harmonic amplitudes than if Lua were used directly.

The example script defines an eight-pole radial magnetic bearing parametrically. The eight-pole bearing is perhaps the most common magnetic bearing geometry. The parameters in the example script correspond the experimental test rig described in [1] and [2]. This same experimental rig is described in deeper detail in [3]. By changing the parameters in the script, just about any eight-pole bearing could be analyzed under any desired set of steady-state operating currents.

The example script specifies an analysis at 30,000 RPM, which is directly comparable to the loss results shown in Figure 7 of [1]. This figure predicts a loss of 34.6 W/A² at 30,000 RPM. Under the same conditions, the script predicts 34.0 W/A². Some difference is expected, because the script incorporates a more detailed and accurate model of fringing around pole tips than the analysis in [1] and [2], which limited itself to an annular solution domain close to the rotor’s surface.

The windage model of NASA TN D-4849 is also implemented in the script to provide an estimate of windage losses. For this case, air at 20°C and 1 atm was assumed. In this case, a windage loss of 250W was calculated.

Conclusions

An Octave worksheet has been presented which allows the computation of radial magnetic bearing rotating losses in FEMM. Predictions closely agree with previous results derived from a special-purpose boundary element program based on a magnetic scalar potential formulation.

References

[1] D. Meeker, A. Filatov, and E. Maslen, “Effect of magnetic hysteresis on rotational losses in heteropolar magnetic bearings,” IEEE Transactions on Magnetics, 40(5):3302-3307, Sept. 2004.

[2] D. Meeker and E. Maslen, “Prediction of rotating losses in heteropolar radial magnetic bearings,” ASME Journal of Tribology, 120(3):629-636, July 1998.

[3] M. E. F. Kasarda, “The measurement and characterization of power losses in high speed magnetic bearings”, Dissertation, University of Virginia, 1997.

Finite Element Method Magnetics : BearingLoss