OctaveFEMM Example: Air Core Coil Inductance Calculation
David Meeker
July 28, 2006
Introduction
As an example of the way that Octave can be use to automate calculations in FEMM, an Octave function is presented which uses FEMM to computes the inductance of a cylindrical air-cored coil of arbitrary dimensions. For comparison, an empirical formula for inductance is implemented in a second Octave function
Finite Element Inductance Calculation
The Matlab function below computes the inductance of an arbitrary coil:
openfemm;
newdocument(0);
mi_probdef(0,'inches','axi',1e-8,0,30);
mi_drawrectangle(ri,-z/2,ro,z/2);
r=2*max([ro,ri,z]);
mi_drawarc(0,-r,0,r,180,5);
mi_drawline(0,-r,0,r);
mi_addcircprop('icoil',1,1);
mi_addblocklabel((ri+ro)/2,0);
mi_addblocklabel(0.75*r,0);
mi_addmaterial('coil',1,1,0,0,0,0,0,1,0,0,0);
mi_addmaterial('air' ,1,1,0,0,0,0,0,1,0,0,0);
mi_addboundprop('abc',0,0,0,0,0,0,1/(r*0.0254*pi*4.e-7),0,2);
mi_selectlabel((ri+ro)/2,0);
mi_setblockprop('coil',0,r/20,'icoil',0,0,n);
mi_clearselected;
mi_selectlabel(0.75*r,0);
mi_setblockprop('air',0,r/100,'<None>',0,0,0);
mi_clearselected;
mi_selectarcsegment(r,0);
mi_setarcsegmentprop(5,'abc',0,0);
mi_saveas('c:\\femm42\\examples\\tmp.fem');
mi_analyze;
mi_loadsolution;
c=mo_getcircuitproperties('icoil');
y=c(3);
closefemm;
The function takes as arguments n, the number of turns in the coil; ri, the inner radius of the coil in inches; ro, the outer radius of the coil in inches, and z, the axial length of the coil in inches.
The function creates the coil’s cross-section inside a spherical region which has a radius of twice the largest dimension of the coil. An “asymptotic boundary condition” is applied to the boundary of the spherical region to mimic the behavior of unbounded space, i.e. so that the finite solution domain has no great effect on solution accuracy. A “circuit”, icoil, is defined carrying one amp. A region with n turns is assigned to the coil, and the region outside the coil is defined as air.
The function analyzes the geometry and loads the solution into the postprocessor. One of the computed properties of icoil is flux linkage. Since the coil current is one amp, the coil inductance is numerically the same as the flux linkage.
Empirical Formula
A more detailed discussion of the Wheeler Formula for the inductance of a multi-turn air cored solenoid is presented at http://home.earthlink.net/~jimlux/hv/wheeler.htm. With the following definitions:
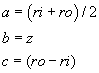
an empirical fit of coil inductance is:
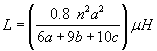
where again, ri, ro, and z are in units of inches. An Octave function that implements the Wheeler formula is wheeler.m
Comparison
In several tests considering coils a square cross-section, a tall, thin coil, and a short, fat coil, similar answers are obtained by both FEMM and the applicable Wheeler formula.
|
Dimensions |
FEMM Inductance |
Wheeler Formula |
|
n=100,ri=1,ro=2,z=1 |
0.64707 mH |
0.64286 mH |
|
n=100,ri=1,ro=1.25,z=4 |
0.23081 mH |
0.22376 mH |
|
n=100,ri=0.25,ro=2,z=0.25 |
0.40955 mH |
0.38208 mH |