Open Boundary Example
Introduction
As of 25Aug2013, FEMM includes a wizard for implementing a new open boundary method, Improvised Asymptotic Boundary Conditions (IABCs). Although this class of open boundary condition can be implement without any special coding, the wizard automatically constructs the boundary region for you, saving time and the possibility of implementation errors.
Example
This note considers the analysis of two magnets connected by a low carbon steel bar, as shown in Figure 1. The a completed example is also available for download (MyMagnet.fem).
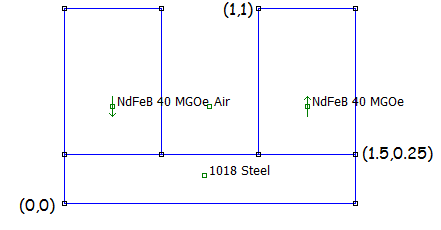
Figure 1: Input Geometry.
For the purposes of the example, 40MGOe magnets were selected with a 0.5" X 0.75" cross-section. The steel bar, assumed to be 1018 grade, has a 0.25" X 1.5" cross-section. The lower left edge of the geometry is placed at (0,0).
Once the magnet is drawn, it is time to run the Open Boundary Builder wizard. The wizard is run by clicking the toolbar with concentric rings, as shown in Figure 2:
Figure 2: Open Boundary Builder toolbar button.
When the button is pushed, the dialog shown in Figure 3 pops up.
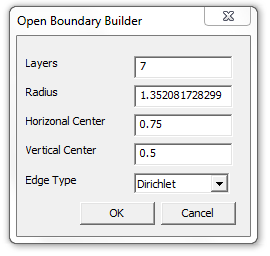
Figure 3: Open Boundary Builder dialog.
The Layers edit box denotes the number of layers in the IABC. In general, the more layers, the more accurate the boundary condition. The specified number of layers can be any integer between 1 and 10. The wizard defaults to 7 layers, implying that the boundary will exactly match the impedance of an unbounded space for up to the 7th spatial harmonic of the magnetic field.
The Radius, Horizontal Center, and Vertical Center describe the radius and center of a circle that closes the domain of interest (i.e. in this case, the C-core magnet). The program automatically computes a bounding box for all objects in the input geometry. The program then selects the center of the bounding box as the suggested center, and 3/4 the length of the diagonal of the bounding box is suggested as the radius of the solution region. However, these values can be user-modified if desired, simply by typing different values in the edit boxes.
The last selection is the Edge Type drop list, from which the user can select either Dirichlet or Neumann. The Dirichlet condition assumes that the unbounded space is "grounded at infinity" (the potential is zero at infinity), whereas the Neumann condition assumes that unbounded space is "insulated at infinity" (zero gradient at infinity, but not a prescribed potential). When in doubt, simply accept the suggested edge type--a reasonable selection is made by default.
After the button is pressed, a series of concentric rings will appear that implement the Improvised Asymptotic Boundary Condition, as shown in Figure 4. No more boundary conditions need be applied, and the problem is ready to solve.
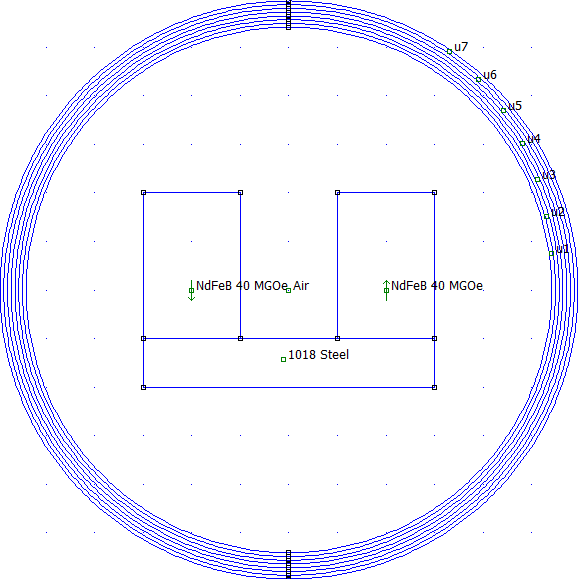
Figure 4: Geometry with IABC generated by the Open Boundary Builder.
The solution is shown below as Figure 5. It can be observed that the magnetic field lines pass the boundary of the modeled region in the same way that they would as if the magnet were truly in unbounded space.
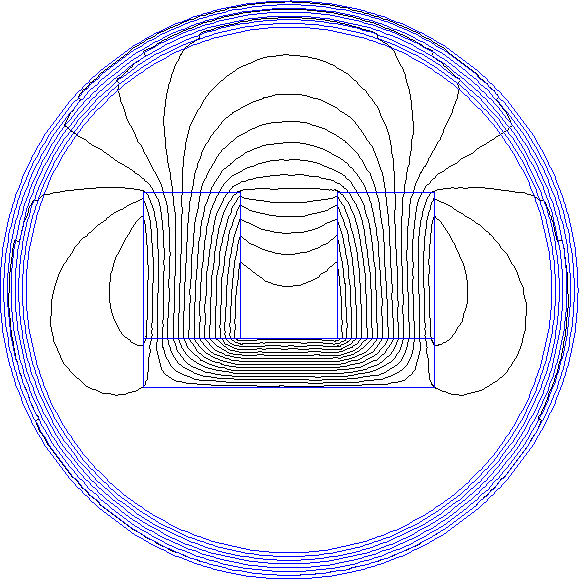
Figure 5: Open boundary solution via IABCs.
Programmatic Implementations
A version of the Open Boundary Builder can also be invoked from any of the programmatic interfaces to FEMM--Lua, Mathematica, Matlab/Octave, or Scilab. The Lua implementation is:
mi_makeABC(n,R,x,y,bc) creates a series of circular shells that emulate the impedance of an unbounded domain (i.e. an Improvised Asymptotic Boundary Condition). The n parameter contains the number of shells to be used (should be between 1 and 10), R is the radius of the solution domain, and (x,y) denotes the center of the solution domain. The bc parameter should be specified as 0 for a Dirichlet outer edge or 1 for a Neumann outer edge. If the function is called without all the parameters, the function makes up reasonable values for the missing parameters. For example, it is permissible to simply call mi_makeABC() to generate an IABC boundary using default parameters.
Note that other problem types have analogous Open Boundary Builder functions: ei_makeABC, hi_makeABC, and ci_makeABC for electrostatics, heat flow, and current flow problems, respectively.
Conclusions
This example demonstrates FEMM's Open Boundary Builder wizard. If a high order IABC is employed (as is the default in the Open Boundary Builder), accuracy rivals the Kelvin Transformation technique. However, solution times are a bit faster than Kelvin Transformation, because the solution domain is a bit smaller and no time is needed in the solver to implement the periodic boundary conditions associated with the implementation of the Kelvin Transformation.